Practical Optimization Methods
Optimization is the core operation of many algorithms in modern applications and fields: Machine Learning, Deep Learning, Computer Vision, Signal and Image Processing, Economic Models, etc…
Optimization is about the ability to formulate and a problem in a manner which allows us to employ an efficient computational framework to solve the problem.
As such, Optimization is a fundamental skill to any algorithm developer in the modern fields.
Learning the ecosystem of modern optimization is the way to gain this ability in order to build efficient systems.
The course deals with practical and modern Optimization methods. It focuses on solving real world problems which are common in Signal and Image Processing, Estimation, Computer Vision and Machine Learning.
The course is accompanied with JuPyteR Notebooks with real world data examples.
Overview
This is a 6 days course for developers (Software Engineers, Algorithm Engineers, Data Engineers, Data Scientists) which introduces them to practical methods, algorithms, tools, frameworks, concepts and strategies in the optimization world.
The course:
${\color{lime}\surd}$ Gives a deep understanding of the concepts and building blocks of algorithms of optimization.
${\color{lime}\surd}$ Introduces some key tools, algorithms and approaches of modern optimizations.
${\color{lime}\surd}$ Demonstrates through Hands On exercises how to formulate and solve real world problems.
${\color{lime}\surd}$ Includes 50 interactive notebooks to exercise the material.
The course will accompanied with a GitHub repository where all notebooks / scripts will be available to the participant.
Main Topics
${\color{lime}\surd}$ Fundamentals: Linear Algebra, Probability, Calculus.
${\color{lime}\surd}$ Convex and Non Convex optimization.
${\color{lime}\surd}$ Smooth and Non Smooth optimization.
${\color{lime}\surd}$ Linear and Non Linear optimization.
${\color{lime}\surd}$ Tools, Frameworks: DCP, CVXPY, CVX, Convex.jl, Optimizers and Solvers.
${\color{lime}\surd}$ Demonstrates results on real world data using battlefield learned tricks with Jupyter Notebooks and hands on approach.
| Fundamentals | Linear Algebra, Probability, Calculus |
| Convex and Non Convex Optimization | Sets, Functions, Epigraph |
| Problem Formulation | Atom Operations, Disciplined Convex Optimization (DCP) |
| Smooth and Non Smooth Optimization | Sub Gradient, Proximal Operator, Composition Model |
| Linear and Non Linear optimization | Acceleration Methods, Non Linear Least Squares |
| Tools & Frameworks | DCP, CVXPY, CVX, Convex.jl, Optimizers and Solvers |
| Real World Problems | Super Resolution, Clustering, Smoothing, Piece Wise Linear Least Squares |
Goals
- The participants will be able to implement advanced algorithms in optimization.
- The participants will be able to formulate and solve real world problems.
- The participants will be able to classify the type of the problem: Continuous / Integer, Smooth / Non Smooth, Linear / Non Linear.
Pre Built Syllabus
We have been given this course in various lengths, targeting different audiences.
The final syllabus will be decided and customized according to audience, allowed time and other needs.
| Day | Subject | Details |
|---|---|---|
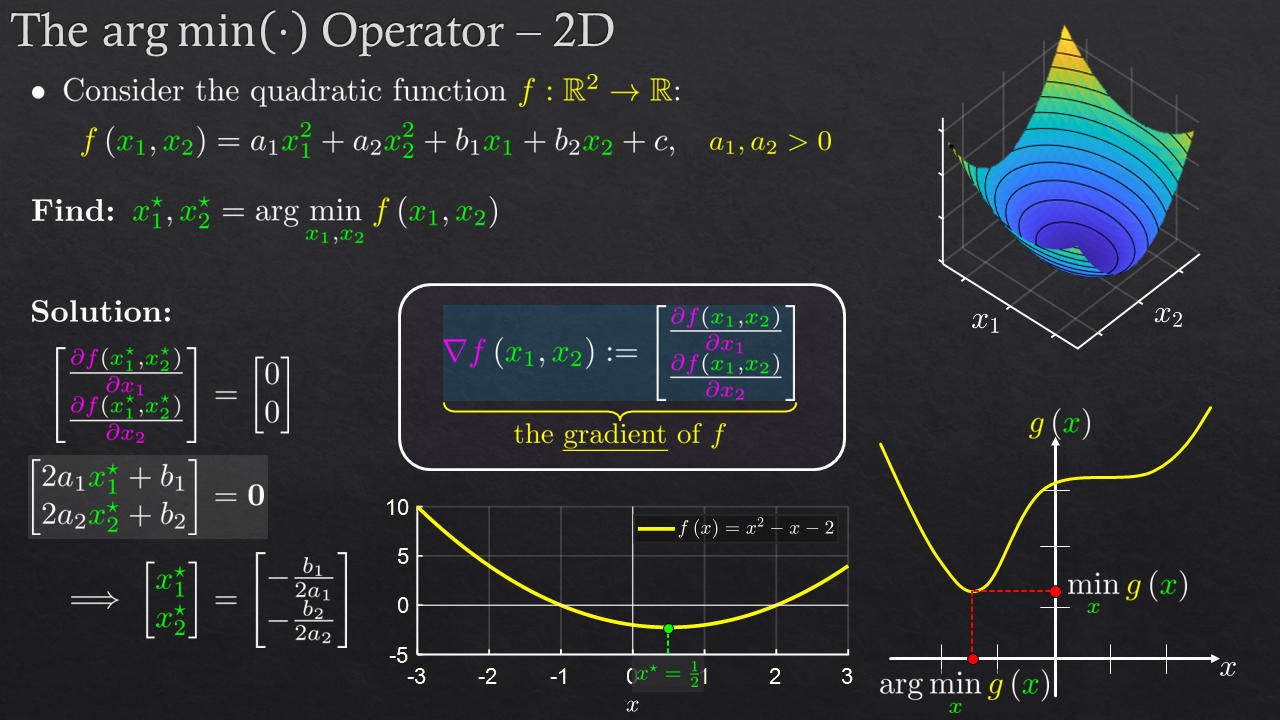
| 1 | Optimization Overview | Motivation, Problems, Problem Types, The $\arg \min$ Operator |
| Math Fundamentals - Linear Algebra | Vector Space, Distance Function, Norm Function, Inner Product, The Matrix Operator | |
| Notebook 001 | The ${L}^{p}$ Norm | |
| Math Fundamentals - Probability | Probability Space, Discrete & Continuous Random Variable, PMF, PDF, CDF, Expectation, Correlation | |
| Math Fundamentals - Estimation | The Likelihood Function, ML Estimator, Bayesian Estimation, MMSE Estimator, MAP Estimator | |
| Notebook 002 | The Maximum A Posteriori (MAP) Estimator | |
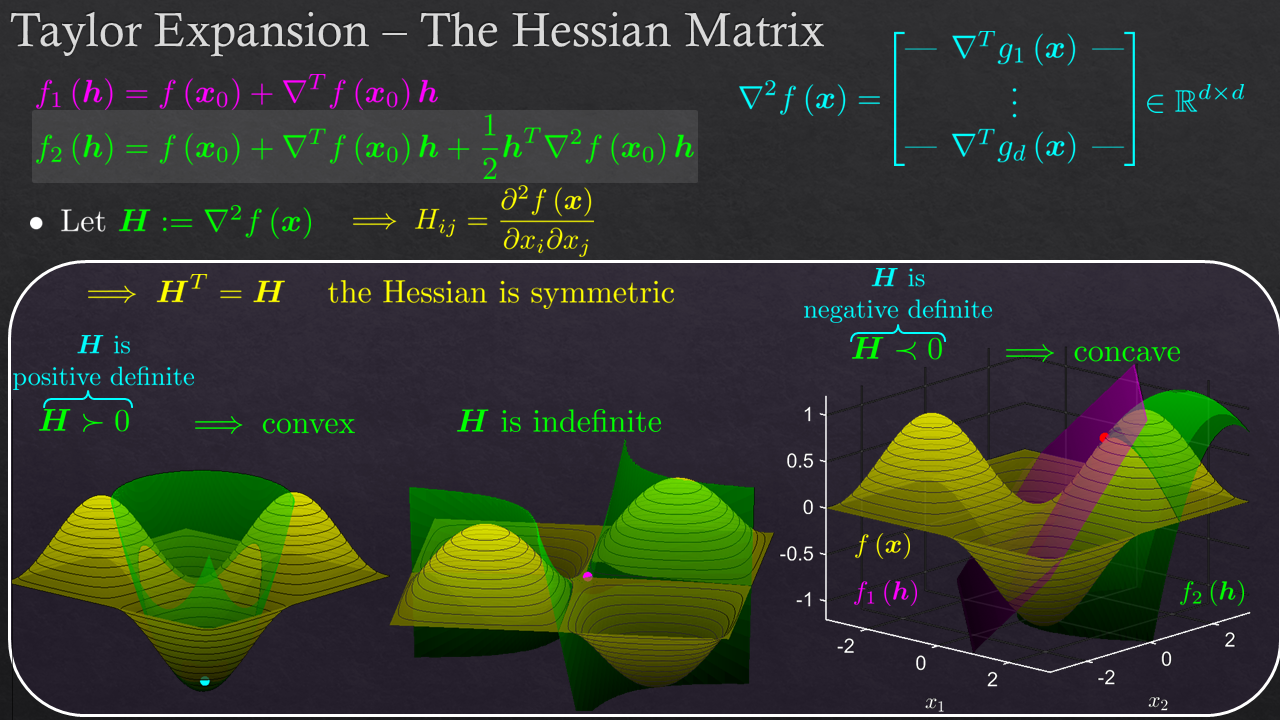
| Math Fundamentals - Matrix Calculus | The Derivative, The Gradient, Directional Derivative, Calculating the Gradient | |
| Notebook 003 | Auto Differentiation (Python) | |
| Notebook 004 | Numerical Differentiation | |
| Objective Functions | Loss functions, Norm induced, Probability Induced, Types of Problems | |
| Notebook 005 | Loss Functions, Gradients | |
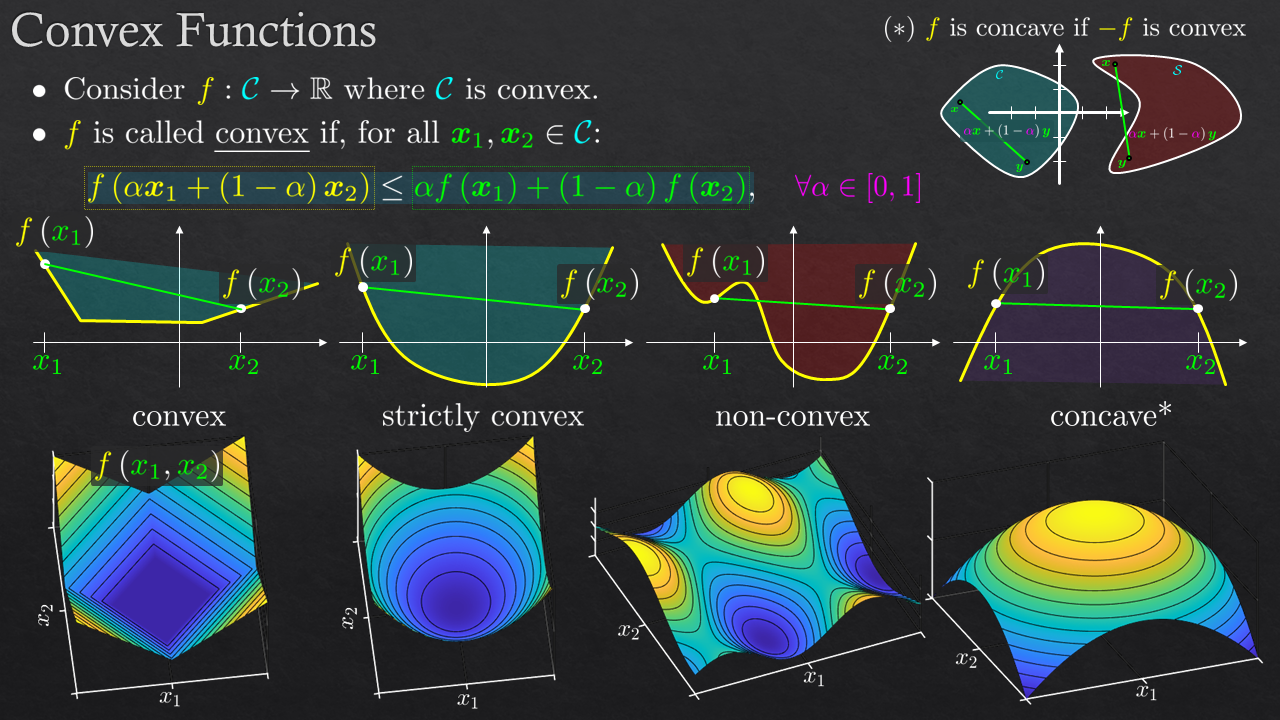
| 2 | Convex Optimization - Foundations | Convex Set, Balls, Convex Function, Convex Problem, Convex Patterns, The Projection Operator |
| Convex Optimization - Smooth Optimization | Gradient Descent, Steepest Descent (Different Norms), Coordinate Descent, Step Size, 1D Methods | |
| Notebook 006 | Gradient Descent for Quadratic Objective | |
| Notebook 007 | Local Quadratic Interpolation | |
| Notebook 008 | Coordinate Descent for Linear Least Squares | |
| Notebook 009 | Logistic Regression | |
| 3 | Convex Optimization - Constrained Optimization | Lagrangian, MinMax Theorem, Duality, KKT, DCP, Linear Programming, Quadratic Programming |
| Notebook 010 | DCP Solver - Bounding Sphere | |
| Notebook 011 | Projected Gradient Descent for LS with Linear Equality | |
| Notebook 012 | Data Fitting with ${L}_{1}$ Norm as Linear Programming | |
| Notebook 013 | Data Fitting with ${L}_{\infty}$ Norm as Linear Programming | |
| Notebook 014 | Least Squares on the Probabilistic Unit Ball | |
| Convex Optimization - Non Smooth Optimization | The Sub Gradient, The Composition Model, The Proximal Operator | |
| Notebook 015 | Sub Gradient Method - Minimizing the Maximum of a Set of Functions | |
| Notebook 016 | Least Squares with ${L}_{1}$ regularization (LASSO Model) | |
| Notebook 017 | Least Squares with ${L}_{\infty}$ regularization | |
| Notebook 018 | Least Squares with ${L}_{0}$ regularization (Sparse Model) | |
| 4 | Convex Optimization - Modern Algorithms & Solvers | Projected Gradient Descent, Proximal Gradient Descent, Acceleration (FISTA), ADMM, PD3O, DCP Solvers |
| Notebook 019 | Total Variation Denoising 1D - FISTA Acceleration | |
| Notebook 020 | Total Variation Denoising 1D - ADMM (Compared to FISTA) | |
| Notebook 021 | Projection Feasibility (Consensus Trick) - Projection onto Intersection of Sets | |
| Notebook 022 | Total Variation Deblurring 1D | |
| Notebook 023 | Piece Wise Linear Model with Auto Knot Selection | |
| Three Operators Composition Problem | 3 Terms ADMM, PD3O, Large Scale Problems, Linear Operators | |
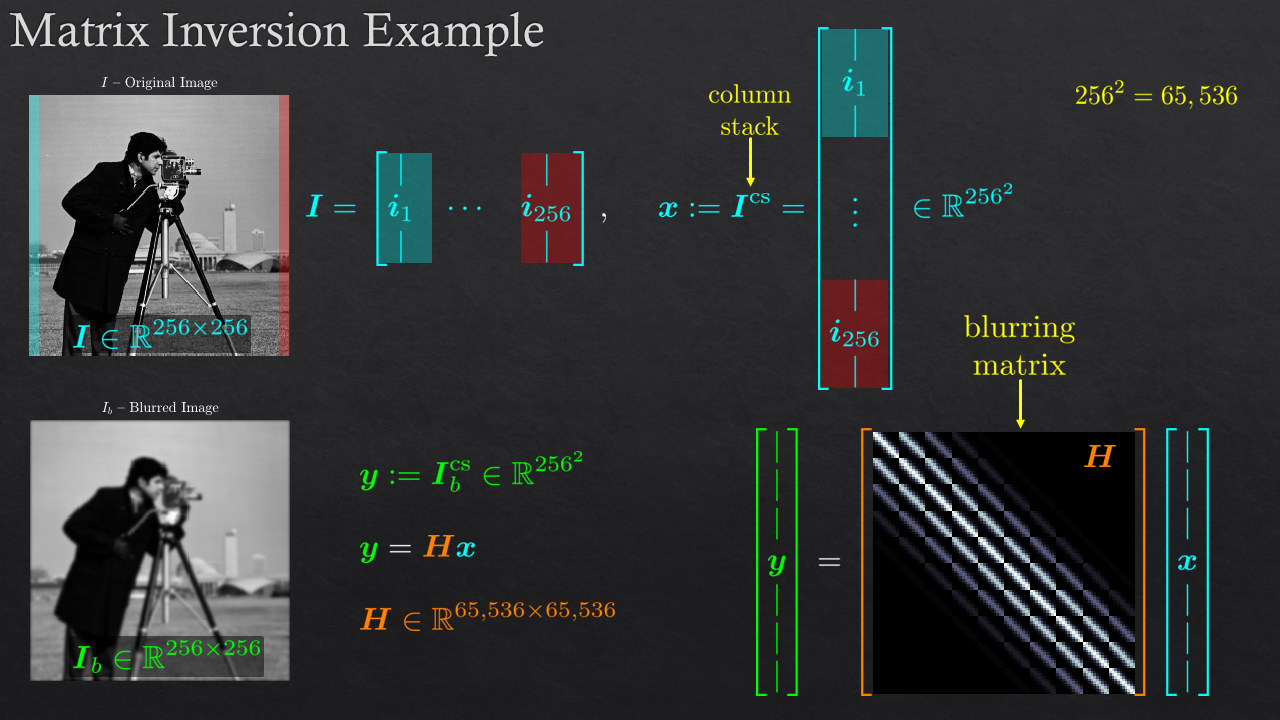
| Notebook 024 | Total Variation Deblurring 2D | |
| 5 | The SVD and Linear Least Squares | The Normal Equations, The SVD, Sensitivity, Weighted LS, Regularized LS, Total Least Squares |
| Notebook 025 | Image Compression using the SVD (Rank) | |
| Notebook 026 | The SVD and Pseudo Inverse | |
| Notebook 027 | Linear Least Squares with Multiple Inputs | |
| Notebook 028 | Weighted Least Squares for Trigonometric Polynomials | |
| Notebook 029 | Regularized Least Squares - Overfitting | |
| Notebook 030 | Sequential LS | |
| Notebook 031 | Sequential Solution to ${L}_{2}$ Regularized LS | |
| Notebook 032 | Total Least Squares for Model Robust Regression | |
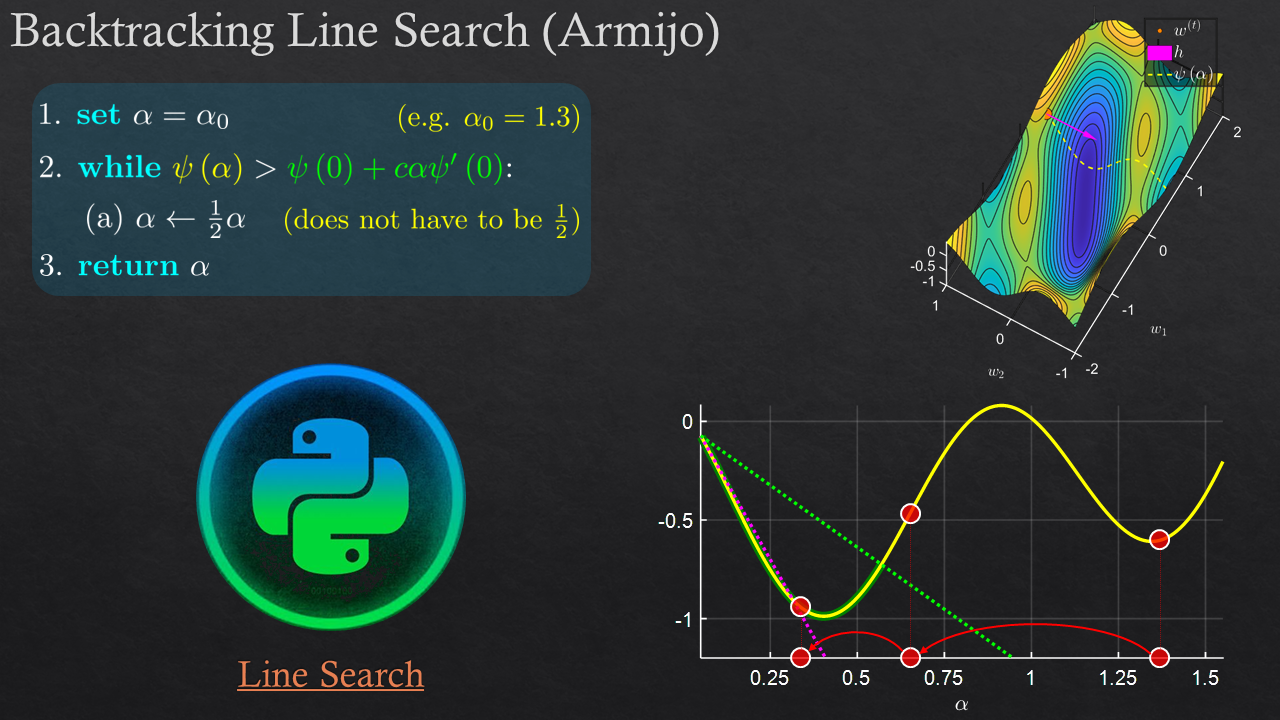
| Non Linear Least Squares | Formulation, Problems, Challenges, Methods: First Order, Second Order, Line Search, Combined Methods | |
| Notebook 033 | Estimation of Harmonic Signal Parameters | |
| Notebook 034 | Estimation of Sum of Harmonic Signals Parameters | |
| 6 | Loss Functions | Smooth, Non Smooth, Sparse Promoting, Regularization, Priors (Probabilistic Point of View) |
| Notebook 035 | Frequency Super Resolution 001 | |
| Notebook 036 | Frequency Super Resolution 002 | |
| Extended Methods - Robust Regression | Robust Regression Methods, RANSAC | |
| Notebook 037 | Robust Regression Using RANSAC | |
| Extended Methods - Large Scale | Matrix Inversion Free Methods (CG), Operators, Stochastic Gradient Descent, Momentum Methods | |
| Notebook 038 | Momentum and Adam Methods for Stochastic Gradient Descent | |
| OPT | Extended Methods - Majorization Minimization | Definition, Generalization of EM |
| Notebook 039 | Multidimensional Scaling (MDS) for Dimensionality Reduction | |
| OPT | Extended Methods - IRLS | Fixed Point Methods, Iterative Reweighted Least Squares |
| Notebook 040 | Linear Equation with ${L}_{\infty}$ Norm | |
| Notebook 041 | LASSO: IRLS vs. Coordinate Descent | |
| OPT | Extended Methods - Non Negative Matrix Factorization | Problem Definition, Approaches |
| Notebook 042 | Recommendation System by NNMF | |
| OPT | Dynamic Programming | Introduction, Examples |
| Notebook 043 | Segmented Linear Least Squares by Dynamic Programming | |
| OPT | Extended Methods - Global Optimization | Local vs. Global, Grid Search, Random Search, Multi Resolution & Fine Tuning |
| Notebook 044 | Non Linear Least Squares for Localization with Coarse to Fine Multi Scale | |
| OPT | Intro to Discrete Optimization | Definition, Convexification, Relaxation, Solvers |
| Notebook 045 | Solving Sudoku Using Binary Linear Programming | |
| Notebook 046 | Clustering using Non Continuous Optimization | |
| OPT | Harmonic Signals Parameter Estimation | Real case, Complex case, Maximum Likelihood, Initialization, Estimators |
| Notebook 047 | Solving composition of 1, 2, 3 and 5 components | |
| OPT | Dictionary Learning | Problem definition, Sparsity measures, Solvers: Matching Pursuit (MP), OMP, K-SVD |
| Notebook 048 | Dictionary Learning for signal classification | |
| Notebook 049 | Online dictionary learning | |
| OPT | Laplacian Eigenmaps for Dimensionality Reduction | Graph, Distance on Graph, Min Cut / Max Flow, Relaxation, The Laplacian Graph |
| Notebook 050 | Dimensionality reduction using Laplacian Eigenmaps | |
| Notebook 051 | Bio Signals clustering using Laplacian Eigenmaps |
Items marked as OPT are optional for customization of the course.
Audience
Algorithm Developers: Machine Learning, Signal Processing, Image Processing, Computer Vision, RF, Data Scientists, Statisticians.
Prerequisites
We can offer this course in MATLAB, Julia or Python.
- Linear Algebra (Basic).
- Probability / Statistics (Basic).
- MATLAB / Python / Julia.
In any case any of the prerequisites are not met, we can offer 1-2 days sprint on: Linear Algebra, Probability and MATLAB / Julia / Python.